Test u Word formatu preuzmite na linku ispod (nastavni listić).
Priprema za prvi pismeni zadatak
Резултат теста
1. Ako je koeficijent sličnosti 0,2, a dužina stranice prvog trougla 10 cm, kolika je dužina odgovarajuće stranice drugog trougla? (Dva tačna odgovora)
2. Ako je |AD|=6 cm, |AC|=16 cm, |DE|=15 cm i |BC|=2 dm. Odaberi NEtačnu jednakost:
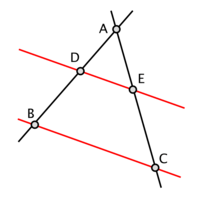
Obim trougla ADE je 33 cm
|DB| = 8 cm
|AB| = 8 cm
|DB| = 2 cm
|AE| = 12 cm
3. U kakvom su odnosu dužine odgovarajućih stranica sličnih trouglova?
4. Dva pravougla trougla uvek su slična.
5. Ako nekom trouglu povećamo dužinu svake njegove stranice 4 puta, koliko se puta poveća obim toga trougla?
6. Odredi visinu čoveka na slici (označenu sa x).
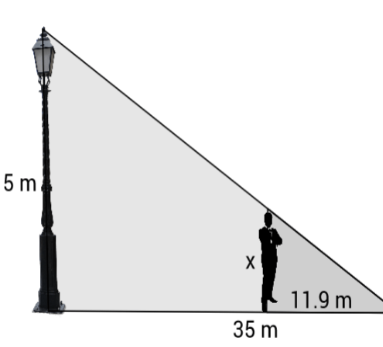
1.7 m
14 m
2.01 m
2.94 m
7. Zadan je trougao stranica dužina 6; 9; 8. Koeficijent sličnosti je 2. Stranice sličnog trougla su:
8. Stranice zadanog trougla su dužina 12, 24, 30. Najkraća stranica sličnog trougla je dužine 16. Najduža stranica sličnog trougla je:
9. Koliko iznosi a'?
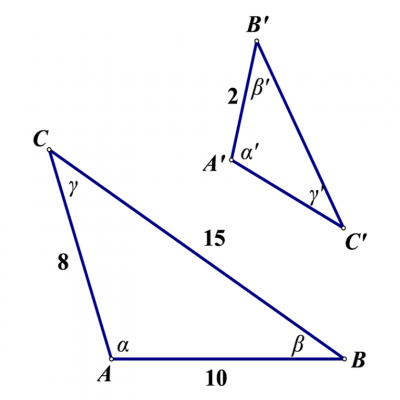
3
2
4
10. Ako dužine stranica jednog trougla iznose 13cm, 17cm i 20cm, a drugog 19.5cm, 25.5cm i 30cm, ta su dva trougla slična.
11. Kolika je visina zgrade koja ima senku dugu 15 m ako čovek visok 1.80 m u tom trenutku ima senku dugu 0.8 m?
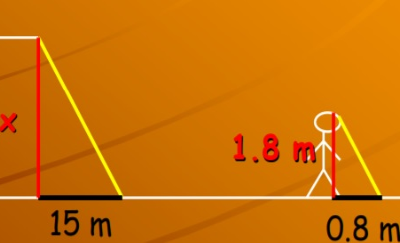
33,75
36,75
33,85
12. Dužine stranica trougla ABC iznose a= 4.5cm, b=7.5 cm, a dužine njemu sličnog trokuta iznose b′=9cm i c'=10.8 cm. Koliki je koeficijent sličnosti manjeg trougla prema većem?
13. Koliko iznose e i c ako je a = 8 cm, b = 2 cm, d = 6 cm f = 25 cm?
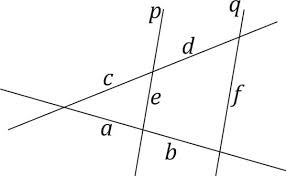
c = 24 cm, e = 20 cm
c = 25 cm e = 24 cm
c = 100 cm e = 20 cm
c = 20 cm e = 24 cm
c = 20 cm e = 100 cm
14. Jesu li trouglovi Δ ABC i Δ A`B`C` slični ako su dužine njihovih stranica: a=11 cm, b=5 cm, c= 4 cm, a`=44 cm, b`=20 cm, c`=18 cm?
15. Dužine stranica prvog trougla iznose a=5cm, b=4 cm i c=7 cm, a najduža stranica njemu sličnog trougla je 140 m. Upiši obim njemu sličnog trougla (u metrima):
16. Visina na hipotenuzu pravouglog trougla deli hipotenuzu na delove dužina 9 cm i 16 cm. Upiši dužinu najkraće stranice trougla:
17. Razmera dužina odgovarajućih stranica dva slična trougla iznosi 3:4. Dužine stranica većeg trougla iznose 12 cm, 16 cm i 20 cm. Kolike su dužine stranica manjeg trougla? Napomena: upiši samo redom mere dužina stranica od najkraće do najduže (npr. 2, 3, 4)
18. Ако је АВ = 8 cm i АВ:ВМ=4:3, ВМ је:
19. Šta sve od navedenog može biti ortogonalna projekcija trougla?
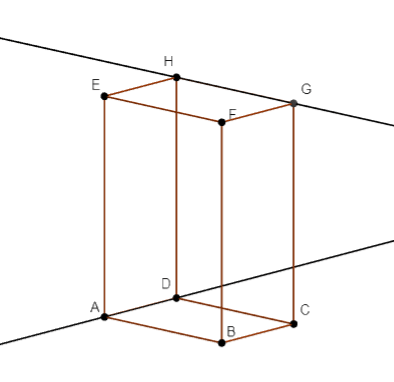
20. Na kvadru ABCDEFGH istaknuta je ravan ABC. Odredi ortogonalnu projekciju četvorougla AFGD na tu ravan.
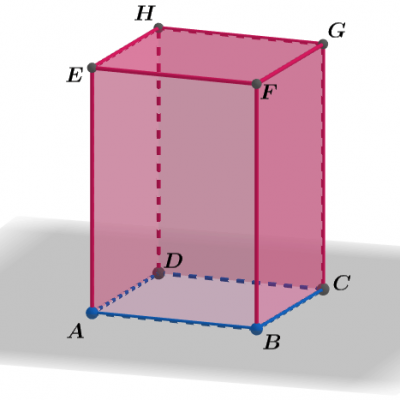
strana ABCD
dijagonala AC
ivica AD
ravan ABC
21. Na kvadru ABCDEFGH istaknuta je ravan ABC. Odredite ortogonalnu projekciju strane ABFE na tu ravan.

duž AB
strana ABCD
Tačke A i B
prava AB
22. Tačke A i B nalaze se s različitih strana ravni π. Udaljenost tačke A od ravni je 8 cm, a tačke B je 4 cm. Dužina duži AB je 20 cm. Kolika je dužina ortogonalne projekcije duži na tu ravninu?
23. Dužine ivica kvadra ABCDEFGH su |AB| = 6 cm, |BC| = 8 cm i |AE| = 15 cm. Odredi dužinu ortogonalne projekcije duži EB na ravan BCD.
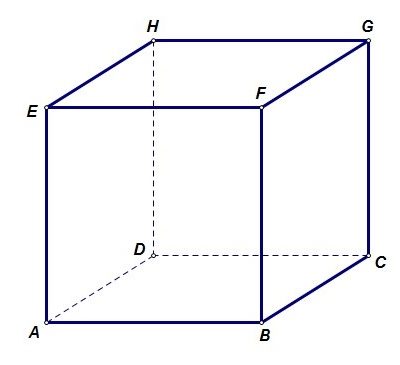
6 cm
8 cm
4 cm
24. Prava određena tačkama A i B seče projekcijsku ravan pod uglom od45°, ako su A i B sa iste strane projekcijske ravni i udaljene od nje 6√6 cm i 14√6 cm, odredi dužinu projekcije duži AB na projekcijsku ravan.
16√3
16√2
16√4
8
25. Prava određena tačkama A i B seče projekcijsku ravan pod uglom od 60° Ako su A i B sa iste strane projekcijske ravni i dužina projekcije duži AB na projekcijsku ravan4√6 cm, odredi dužinu duži AB.
26. Prava AD je presek ravni BCD i AEF.
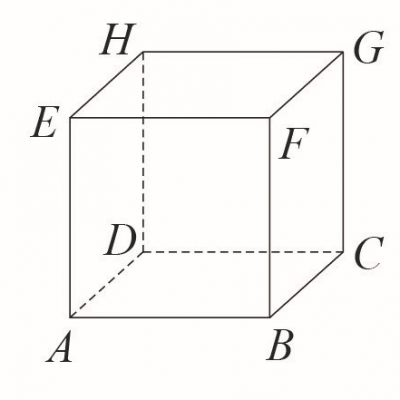
ne
da
27. Koje prave, koje prolaze ivicama kocke, su mimoilazne prave sa pravom FG?

AB, CD, EA, DH,
AC, BG, DC, DH,
AB, AD, AE, GH,
AC, CE, BH ,DB
28. Dve ravni se seku:
29. Ravan može biti zadana sa:
30. Prave HG i AD
se mimoilaze
su normalne međusobno
su paralelne
se seku
31. Četiri nekolinearne tačke određuju 4 prave.
32. Koliko pravih određuju 8 tačaka na crtežu?
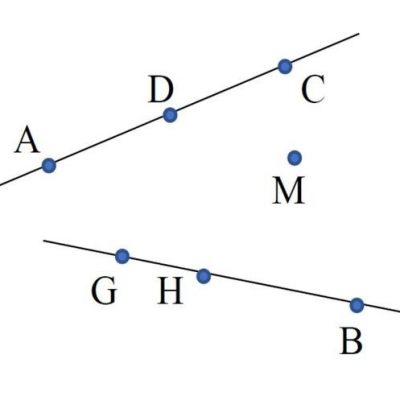
24
25
26
27
33. Koliko pravih određuju 7 tačaka na crtežu?
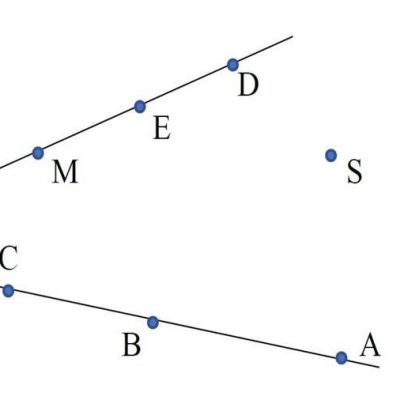
17
18
19
16
34. Koliko najmanje tačaka određuje 105 pravih?
35. Koliko najmanje tačaka određuje 15 pravih?
36. Četiri kolinearne tačke određuju beskonačno mnogo pravih.
ШТА ЖЕЛИШ ДА УРАДИШ?
ВИДИ РЕЗУЛТАТЕ
ПОШАЉИ РЕЗУЛТАТЕ


