Резултат теста
1. Колико најмање страница може имати многоугао? Како зовемо тај многоугао?
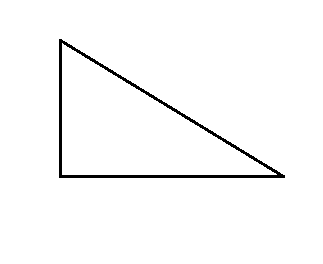
2. Са дате слике одредити колико страница има дати многоугао.
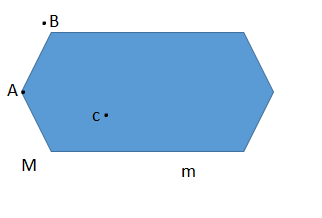
3. На слици је дат многоугао М, многоугаоаона линија m и тачке A,B и C. Уместо * уписати одговарајући знак ϵ или ∉: а) C*M; б)B*M; в) A*m
4. Која од датих фигура није осно симетрична ?
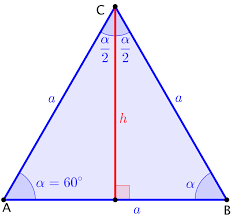
једнакостранични троугао
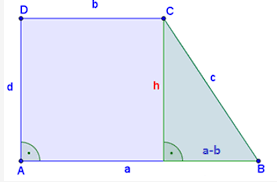
правоугли трапез
коцка
једнакокраки троугао
правоугаоник
ромб
5. Ако се нека фигура пресликава у саму себе у односу на неку тачку, кажемо да је та фигура:
6. Која од датих фигура је централно симетрична?

ромб

једнакостранични троугао

правоугли трапез
7. Колико страница може имати многоугао који може бити само конвексан?
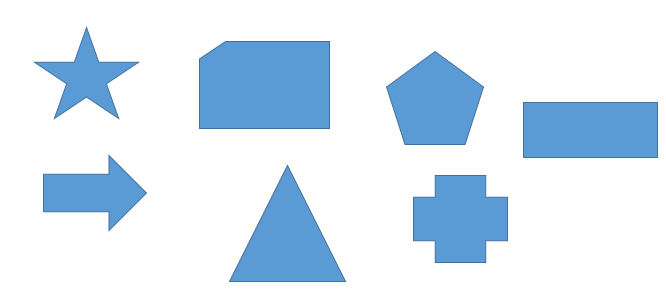
8. На датој слици све фигуре су многоуглови.

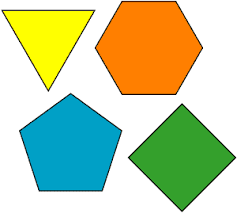
9. На датој слици све фигуре припадају неконвексним многоугловима.
10. Многоуглови су фигуре у равни ограничене и затворене изломљеном линијом, која нема самопресека.
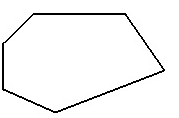
11. Многоугао је ковексан ако садржи сваку дуж чије крајње тачке припадају том многоуглу.
12. Спољашњи угао многоугла је угао суплементан унутрашњем углу многоугла.
ШТА ЖЕЛИШ ДА УРАДИШ?
ВИДИ РЕЗУЛТАТЕ
ПОШАЉИ РЕЗУЛТАТЕ


